Classic LotusScript: When 100.0 isn't 100.0 anymore?!
Today I had to debug some old code, and when doing so I stumbled over something which I found strange.
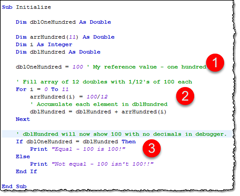
LotusScript would not consider the value 100 equal to the value 100 … Let me explain with some simple code (you can click on every image to get a larger one by the way);
I put the above code in a test-agent.
Marked by 1, I set my reference value to the value 100 (and yes, by purpose I don’t use the forced floating point notation 100.0)
Marked by 2, I fill my array of 12 doubles with 1/12 of 100 each.
Marked by 3, I compare the two variables dblOneHundred and dblHundred.
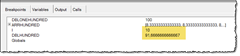
Below you see how the array look in the Designer’s Debugger;
As you see LotusScript does a nice job of converting my division (100/12) and storing it as a doubles. For each time I fill in an element in the array, I accumulate the values in the variable dblHundred. Again LotusScript seems to do this nicely. Below you see what it looks like after I have run the loop 11 times;
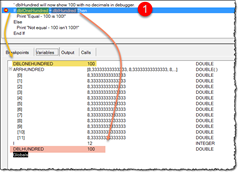
… and when the array is completely filled, the Debugger shows that the variable dblHundred has the accumulated value of 100. Below you see the code just before the comparison line marked by 1 is executed;
As we see in the debugger, both values are shown as 100 in the debugger, and I would believe that the comparison would be true. But no …
If you want to see more, both on my take for an explanation, the workarounds including code to try out, please continue to read below.
What is happening?
Since LotusScript deems these two numbers different, there must be a difference between the two numbers, at least as LotusScript sees it.
My guess is that it has to do with decimal precession in floating point numbers combined with some issue in either on how doubles are stored or when they are compared.
When I force the result of the division 100/12 into each element in my array, the number is 8.33333… with an indefinite number of decimals. According to the LotusScript Help, the Double datatype is a 8-byte floating point value meaning that it can have a huge number of decimals – at least behind the scenes.
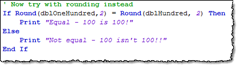
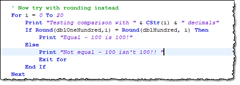
To test this I do the same comparison with the Round-function, like this;
This works and LotusScript says the numbers are equal!
Just for the fun of it, how many decimals can we use before the comparison fails?
14 decimals is the answer.
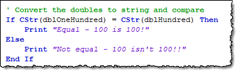
Another thing to try is to simply convert the numbers to text, like this;
This also works.
Somewhere LotusScript have an implementation conflict between the super-precise double value, and what to display and use for other functions. By the latter I mean that we actually see 100 in the debugger, and not 99.9999999something …
Try the following in your OS calculator; Multiply 12 by 8.33 and you get 99.96. Do the same with 8.333333333 (9 decimals) and you get 99,999999996. First with 15 decimals we get 100.
Thus I further guess that LotusScript differs with the number of decimals in the implementation of CDbl compared with the compare-operation (=). If I “overdo” it a little manually, you could say that LotusScript perhaps has stored the month-values with 15 decimals precision, and when it compares the doubles, it only use 14 decimals – or vise versa.
Is this a problem?
Yes!! The problem is first and foremost language consistency. If you you simply can convert the values to text, and then perform an equal comparison, it means that the CStr-function in LotusScript do some sort of “discard the way-off decimals” and it sees the value 100 exactly as that string-wise (and just as the Debugger by the way).
When you compare two doubles like I have shown, and you can’t see the difference in the debugger, neither should the comparison-operator. In a sense it feels like LotusScript utilize some super-precision in one place, while disregarding it in other places.
The impact of this is that I have to find and safeguard my code in a bunch of places.
The code for the test agent
Dim dblOneHundred As Double
Dim arrHundred(11) As Double
Dim i As Integer
Dim dblHundred As Double
dblOneHundred = 100 ' My reference value - one hundred
' Fill array of 12 doubles with 1/12's of 100 each
For i = 0 To 11
arrHundred(i) = 100/12
' Accumulate each element in dblHundred
dblHundred = dblHundred + arrHundred(i)
Next
' dblHundred will now show 100 with no decimals in debugger.
If dblOneHundred = dblHundred Then
Print "Equal - 100 is 100!"
Else
Print "Not equal - 100 isn't 100!!"
End If
' Now try with rounding instead
For i = 0 To 20
Print "Testing comparison with " & CStr(i) & " decimals"
If Round(dblOneHundred,i) = Round(dblHundred, i) Then
Print "Equal - 100 is 100!"
Else
Print "Not equal - 100 isn't 100!! "
Exit for
End If
Next
' Convert the doubles to string and compare
If CStr(dblOneHundred) = CStr(dblHundred) Then
Print "Equal - 100 is 100!"
Else
Print "Not equal - 100 isn't 100!!"
End If


Comments
Posted by Glen At 09:29:19 On 22.02.2017 | - Website - |
this is in portrait mode where 8 decimal places is the maximum that can be typed in
Posted by Don At 14:15:05 On 22.02.2017 | - Website - |
Posted by Robert Ibsen Voith At 14:19:42 On 22.02.2017 | - Website - |
Posted by Robert Ibsen Voith At 14:29:33 On 22.02.2017 | - Website - |